Nymbat is an abstract game for two players (there is also a four player variant). The name “Nymbat” is a combination of the words number and combat.
Rules
Board
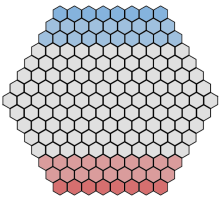
Play on a six-sided hexagonal map with 8 hexes per edge (15 hexes width, see image below).
Home Row:
Each player has a home row of 8 hexes directly next to an edge that is opposite to the opponent’s home row.
Setup Area:
A player’s home row and the next two rows to it are his setup area (three rows, 27 hexes).
Pieces:
There is no fixed set of pieces. Instead, each player creates his pieces from a set of possibilities. Each piece in the game has a color to determine to which player it belongs and a whole number from one to six. Other numbers are not allowed. You can use dice, for example. Pieces are placed inside a hex, with only one piece per hex allowed (except during movement).
Reserve Number:
Each player notes a reserve number of 60 on a piece of paper or using pieces next to the board.
Play
Both players must agree beforehand who will take the first turn. Players alternate taking turns. On each player’s first turn he must bring in reserves with a limit of 30 (see below).
On subsequent turns a player chooses one of the following three options:
- Bring in Reserves
- Move a Group
- Pass
Bring in Reserves:
The player places any number of his pieces on unoccupied hexes in his setup area, but at least one. He may choose the number for each piece (1-6). On his first turn the total of the numbers on the pieces he places may not exceed 30. After his first turn he may place any total if it does not exceed his current reserve number. At the end of his turn he subtracts the total of numbers he placed from his reserve number.
Move a Group:
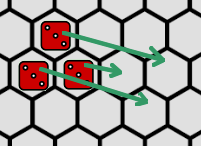
The player may move any or all of his pieces in one contiguous group (a solitary piece is also considered a group). Each piece may move any number of hexes up to the lowest number in the group. A piece does not have to move in a straight line. He must end the movement of a piece before he can move another. Both the selection of pieces and the distance they can move are determined by the group as it was at the start of the turn. Moving a piece during a turn does not change this. A player’s own pieces do not block movement, but they may not end movement together in the same hex. If a player moves a piece into a hex containing an opponent’s piece then he must must end its movement there and do removal and breakthrough (see below) before moving the next piece.
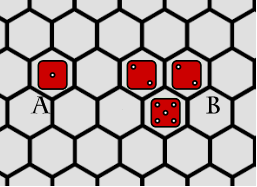
Red player can either move group A one hex or group B two hexes.
Pass:
A player must pass if he has no piece on the board and cannot bring in any new piece. He may also choose to pass.
Removal:
When a piece ends its move in a hex with an opponent’s piece then the opponent’s piece is removed from the board. The moving player’s piece is also removed if the number on his piece is equal to or lower than the number of the opponent’s piece plus the total of opponent pieces’ numbers in adjacent hexes. If it is higher then the moving player’s piece is not removed. See picture.
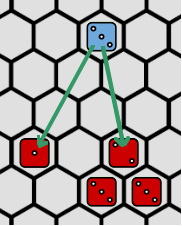
Blue player moves and can either remove the red 1 and keep his piece or remove the red 2 and also lose his piece. The two red 3s are supporting the red 2 for a total of 8.
Breakthrough:
If the removal of an opponent’s piece causes a contiguous group of his pieces to be split into two or more groups then the moving player may remove any or all opponent’s pieces adjacent to that piece with the following limit. The total of numbers of the adjacent pieces removed may not be greater than the number of the last piece the moving player moved. The removal of additional pieces in this way does not cause a “breakthrough” again (i.e. no chain reactions). See picture.
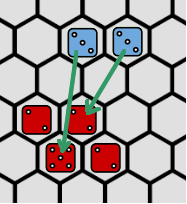
Blue player moves, first removes a red 2 and then the red 5, resulting in breakthrough and so blue can remove one other red 2 piece of his choice. He cannot remove both remaining red 2s because their total is 4 which is greater than 3. Blue loses both his pieces.
Retreat/Delay Penalty:
A player must reduce his reserve number by one if he retreats on one turn or every seven turns he delays (even if non-consecutive). If his reserve number is zero, then he must instead remove one of his pieces from the board (if there still is one there). A turn is considered to be a retreat if a player moves a group effectively further away* from the opponent’s home row. A turn is a delay if none of his groups moved effectively closer* to the opponent’s home row and he did not bring in any new pieces. A pass is also a delay. If the player removes an opponent’s piece on his turn then it is neither a delay nor a retreat in any case. A turn that already is a retreat is also not considered to be a delay in any case.
*) To determine the change of distance to the opponent’s home row compare the start with the end of the turn only and by counting the number of hexes from the closest piece of the group each time. Pieces are considered as belonging to the group as it was at the start of the turn only (i.e. splitting up or moving adjacent to other groups does not change group membership for this rule).
Red is retreating since he moved back one row.

Red is delaying. Although one piece has moved backwards, his most forward piece has stayed on the same row, so it stills counts as a delay.
Win
A player wins the game if at the start of his turn he has a piece on his opponent’s home row and no opponent’s piece is there. If all the pieces on the board have been removed and both players have a reserve of zero, then the player who moved last wins.
Downloads
You can also download a PDF version of the rules (with pictures) here: Nymbat rules.
Also there is a module for the Vassal game engine available (for online play, contact me if you are interested).
Strategy Tips
Here are some elementary hints for better play:
Groups should most often consist of one number. That way you don’t waste any movement points.
Pieces in groups defend better. The numbers of the adjacent pieces add to each to other to create higher numbers which helps deter an attack
Large (and some small) groups are vulnerable against “breakthrough”. “Breakthroughs” against your own pieces should nearly always be avoided
A group which consists of three hexes directly adjacent to each other is safe against a “breakthrough”. This formation (I call it a “shield”) should be chosen when the opponent has higher numbered pieces nearby.
At the start you can put all your pieces in one big group. The opponent is still far away and won’t be able to attack you. This has the advantage that you can move everything in the next turn.
If you still have a reserve number of at least two, then you will not lose if your opponent moves onto your empty home row. You can then bring in two 1s and put them on your home row. Your opponent won’t be able to remove both of them.
Certain numbers are good against certain other numbers. This means that one type of number will usually be able to remove more points or lose less points in a direct confrontation. Memorize which combinations these are. The 3s are good against 6s and 5s, 6s are good vs. 1s, 1s are good vs. 2s, 2s and 4s are good vs. 3s, 2s are good vs. 4s, 5s are good vs. 2s, etc.
Setup for Beginners:
Beginners can choose this setup for their first move (costs 30 reserve points) which is relatively good:
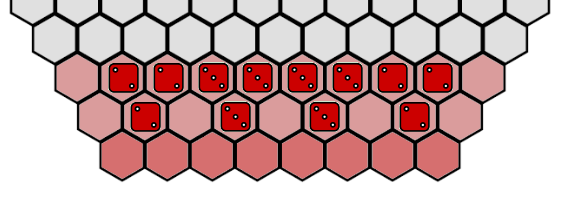
Analysis
I looked more into the possibilities of the first move (setup move). There are at least a billion possibilities just for setting up 1s. If you just count the “reasonable” setups using higher numbered pieces then there are at least a million.
The game appears to have the property of nontransitivity. This would make it an interesting game in my opinion.
Dilemma
At the basis of the game is the dilemma whether to keep your pieces in groups or not.
Advantages of Groups: You want to keep your pieces in large groups so you can move as many pieces on one turn as you can. In groups you also defend better, since adjacent pieces will add their value to force an attacker to lose his piece too.
Disadvantages of Groups: Groups are vulnerable to “Breakthrough”. If your opponents manages to split up your group then you will lose a lot of pieces. With a mixed numbered group you will also waste the movement capability of all numbers higher than the lowest number of the group. Basically, the lowest numbered pieces slows down the other pieces. So you want to split up your groups by number for optimal use of movement distance. Also, there is the less obvious disadvantage of having to move more pieces forward if you have large groups. Every three turns you must move forward or else suffer a penalty. So if you are trying to delay then it is a disadvantage to have large groups.
Balance of Pieces
All pieces seem to be balanced in that they all have a use, at least this is my goal.
The higher numbered pieces are obviously the more powerful ones because they can move further and are less likely to be lost when attacking. The disadvantage of course lies in the amount of those pieces you can have (ie. they cost more reserve points). You can have simply more of the lower numbered pieces. You can also win with a lower numbered pieces just as well as with a higher-numbered one.
Strategy
I’ve already tested the strategy of taking all 6s or all 5s and then just attacking. The counter-strategy to this is to create lots of 3s and form in triangles (I call it a “shield” formation). The “shield” formation of 3s can be destroyed by 6s or 5s but only at a loss of points (ie. as attacker you lose more reserve points than the defender does). 6s are more vulnerable to this than 5s since the difference is bigger. Against a mass of 5s a few 6s are useful as defender since you can threaten counter-breakthrough.
There are two types of groups (with more than a single piece) which are inherently invulnerable to breakthrough. These are the “shield” formation, groups of three directly adjacent pieces, and “twins” formation of two adjacent pieces. Another group of pieces which can be invulnerable to a breakthrough is a line of pieces with sufficient depth (a “horde”). The depth of the line necessary depends upon the highest numbered group of your opponent. If he only has 2s, then a depth of 3 is sufficient, if he has 3s, then you need a depth of 4 and so on. Less depth is needed depending on the move range of your own pieces if you keep the distance.
Groups of 3s can be defeated with a combination of 1s and 4s.
Note that a twins formation in a defensive situation will beat any single piece, even a 6.
A horde of 1s will gradually push back groups of 2s but will easily be defeated by a large enough number of 5s or 6s.
First Move Advantage
I’m not sure whether there really is a first move advantage in this game or not. It could be that the player who moves first is actually at a disadvantage because then the other player knows what pieces to bring in to counter those.

Recent Comments